Quiz 12-1 basic set theory counting outcomes probability – Embark on an academic exploration with Quiz 12-1: Basic Set Theory, Counting Outcomes, and Probability. This comprehensive assessment delves into the fundamental principles that underpin these mathematical concepts, providing a solid foundation for further study and application.
Through engaging questions and real-world examples, we will illuminate the concepts of set theory, counting outcomes, and probability, equipping you with the tools to analyze and solve problems effectively.
1. Set Theory Concepts

Set theory is the study of sets, which are well-defined collections of distinct objects. A set is represented by braces and its elements are listed inside. For example, the set of vowels in the English alphabet can be written as a, e, i, o, u.
Subsets and Set Operations
A subset of a set is a set that contains only elements of the original set. The subset relation is denoted by the symbol ⊆. For example, the set a, e is a subset of the set a, e, i, o, u.
Set operations include union (∪), intersection (∩), and complement (‘). The union of two sets is a new set that contains all elements that are in either of the original sets. The intersection of two sets is a new set that contains only the elements that are in both original sets.
The complement of a set is a new set that contains all elements that are not in the original set.
2. Counting Outcomes
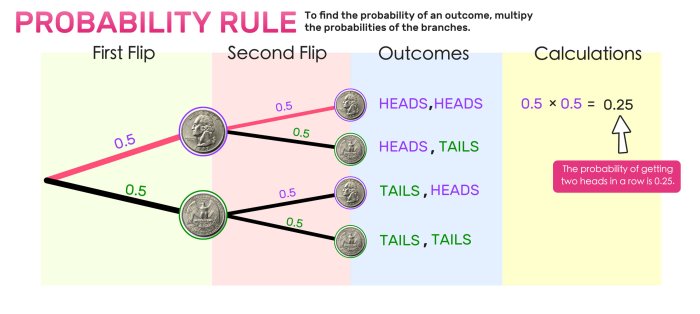
Fundamental Counting Principle
The fundamental counting principle states that if there are n ways to do one thing and m ways to do another thing, then there are n × m ways to do both things in order.
Permutations and Combinations
Permutations are arrangements of objects in a specific order. Combinations are selections of objects without regard to order.
3. Probability Basics: Quiz 12-1 Basic Set Theory Counting Outcomes Probability

Definition and Concepts
Probability is a measure of the likelihood that an event will occur. It is expressed as a number between 0 and 1, where 0 indicates impossibility and 1 indicates certainty.
Sample Space and Events
The sample space of an experiment is the set of all possible outcomes. An event is a subset of the sample space.
Probability Distributions, Quiz 12-1 basic set theory counting outcomes probability
A probability distribution assigns a probability to each event in the sample space.
FAQ Corner
What is the fundamental counting principle?
The fundamental counting principle states that if there are n ways to perform one task and m ways to perform a second task, then there are n x m ways to perform both tasks.
How do you calculate the probability of an event?
The probability of an event is calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
What is the difference between a permutation and a combination?
A permutation is an arrangement of objects in a specific order, while a combination is a selection of objects without regard to order.
